Given:
Zeroes of a polynomial are –2, –4, –3 + 4i.
To find:
The polynomial function of least degree with real coefficients in standard form.
Solution:
According to the complex conjugate root theorem, if a complex number a+ib is a zero of a polynomial, then its conjugate a-ib is also a zero of than polynomial.
–3 + 4i is zero of the polynomial. So, by complex conjugate root theorem -3-4i is also a zero of required polynomial.
If c is a zero of p(x), then (x-c) is a factor of p(x).
–2, –4, –3 + 4i, -3-4i are zeroes of the polynomials. So, (x+2), (x+4), (x+3-4i), (x+3+4i) are the factors of the required polynomial.
Let the required polynomial be p(x), so

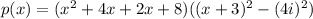
![[\because a^2-b^2=(a-b)(a+b)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/85p639al2fqbkfpvaacm253m69siuprplr.png)
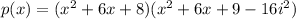
![[\because (a+b)^2=a^2+2ab+b^2]](https://img.qammunity.org/2022/formulas/mathematics/high-school/30v5pzlwcqi892xdjcz1mq364jokft77ac.png)

![[\because i^2=-1]](https://img.qammunity.org/2022/formulas/mathematics/high-school/z24xir88d20yppchswroot2b03adpi65o2.png)
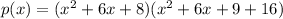
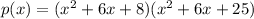

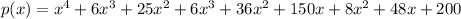
Combining like terms, we get

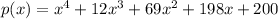
Therefore, the required polynomial is
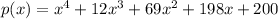 .
.