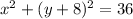Question

Which equations represent circles that have a diameter of 12 units and a center that lies on the y-axis? Select two options. x2 + (y – 3)2 = 36 x2 + (y – 5)2 = 6 (x – 4)² + y² = 36 (x + 6)² + y² = 144 x2 + (y + 8)2 = 36

Answer 1

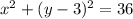`x^2+(y-3)^2=36\\` and
`x^2+(y+8)^2=36`

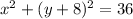
Explanation:

So the general formula for a circle is usually represented as:
`(x-h)^2+(y-k)^2=r^2` where (h, k) is the center of the circle and r is the radius of the circle.

Since the diameter is 12, the radius is going to be 6, because the radius is half the diameter. We now square that value (since it's squared in the equation), you get 36, which is going to be on the right side.

The last thing to know is since it's on the y-axis, that means h=0, since if h didn't equal 1, it would either be to the right or left of the y-axis. So the equation should look something like this:
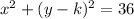`x^2+(y-k)^2=36` where k can be any real number.

So this gives you the two equations:

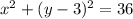`x^2+(y-3)^2=36\\` and
`x^2+(y+8)^2=36`