- (a) Maximum emf: 90 V (2 sig. fig.)
- (b) Emf at π/32 s: 85 V.
- (c) t = 0.125 s.
Step-by-step explanation
(a)
The maximum emf in the coil depends on
- the maximum flux linkage through the coil, and
- the angular velocity of the coil.
Maximum flux linkage in the coil:
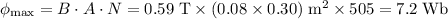 .
.
Frequency of the rotation:
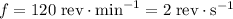 .
.
Angular velocity of the coil:
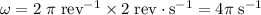 .
.
Maximum emf in the coil:
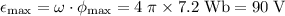 .
.
(b)
Emf varies over time. The trend of change in emf over time resembles the shape of either a sine wave or a cosine wave since the coil rotates at a constant angular speed. The question states that emf is "zero at t = 0." As a result, a sine wave will be the most appropriate here since
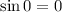 .
.
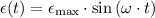 .
.
Make sure that your calculator is in the radian mode.
 .
.
(c)
Consider the shape of a sine wave. The value of
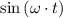 varies between -1 and 1 as the value of
varies between -1 and 1 as the value of
 changes. The value of
changes. The value of
 at time
at time
 depends on the value of
depends on the value of
 .
.
 reaches its first maximum for
reaches its first maximum for
 when what's inside the sine function is equal to
when what's inside the sine function is equal to
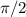 .
.
In other words, the first maximum emf occurs when
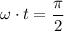 ,
,
where
 ,
,
and
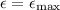 .
.
 .
.