2 Answers

MuriloKunze · Answer 1 · 2020-04-02T14:54:48+0000

Hello!

The answers are:

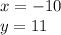
$x=-10\\y=11$

We can solve system of equations using several methods, but the simplest way to solve it, is isolating variables in terms of another variables.

So, isolating "x" from the second equation we have:

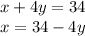
$x + 4y =34\\x=34-4y$

Then, substituting "x" into the first equation, we have:

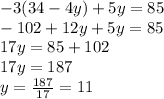
$-3(34-4y) +5y =85\\-102+12y+5y=85\\17y=85+102\\17y=187\\y=(187)/(17)=11\\$

Now, substituting "y" into the second equation to calculate "x", we have:

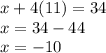
$x + 4(11) =34\\x=34-44\\x=-10$

So, the solutions for the system of equations are:

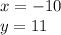
$x=-10\\y=11$

Have a nice day!

Beren · Answer 2 · 2020-04-06T13:42:35+0000

Answer: option C

$x=-10\\y=11$

Explanation:

You can apply the elimination method:

- Multiply the second equation by 3.

- Add both equations to cancel out the variable x.

- Solve for y:

$\left \{ {{-3x+5y=85} \atop {(3)(x+4y)=34(3)}} \right.\\\\\left \{ {{-3x+5y=85} \atop {3x+12y=102}} \right.\\-------\\17y=187\\y=11$

- Substitute y=11 into any of the original equations ans solve for x. Then:

$x+4(11)=34\\x=34-44\\x=-10$