Question

25.............::.....

Answer 1

Hello!

The answer is:

a.
`(x-√(7x))/(x-7)`

Why?

Rationalizing involves eliminating or the roots of both numerator and denominators, there are severals ways to do it but one of the most common methods is using the conjugate term.

We must remember that:

`(a-b)(a+b)=a^(2)-b^(2)`

So, for the given expression:

`(√(x))/(√(x)+√(7))`

The conjugate is:

`√(x)-√(7)`

The, we need to multiply both numerator and denominator (in order to not affect the expression) by the conjugate expression in order to eliminate the radicals in the denominator:

`(√(x))/(√(x)+√(7))*(√(x)-√(7))/(√(x)-√(7))=((√(x))*(√(x)-√(7)))/((√(x)+√(7))*(√(x)-√(7)))`

`((√(x))*(√(x)-√(7)))/((√(x)+√(7))*(√(x)-√(7)))=((√(x))^(2)-(√(x))*(√(7)))/((√(x))^(2)-(√(7))^(2))`

`((√(x))^(2)-(√(x))*(√(7)))/((√(x))^(2)-(√(7))^(2))=(x-√(7x))/(x-7)`

Have a nice day!

Answer 2

Answer: Option a.

Explanation:

1. Multiply the numerator and the denominator of the expression shown in the image, by the conjugate of the denominator (
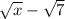`√(x)-√(7)`), as you can see below:

`((√(x))(√(x)-√(7)))/((√(x)+√(7))(√(x)-√(7)))`

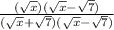
2. By definition, you know that:

`(a+b)(a-b)=a^2-b^2`

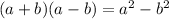
3. Therefore, you obtain the following result:

`((√(x))^2-√(7x))/((√(x))^2-(√(7))^2)=(x-√(7x))/(x-7)`

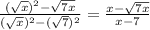
Then, the answer is option a.