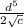Answer:
The answer is (b) ⇒
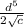
Explanation:
∵
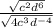
∵ √x² = x ⇒ that means to cancel the square root divide
the power by 2
∴
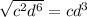
∵ √4 = 2 ⇒ √2×2 = √2² = 2
∵ √c³ =
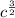
∴
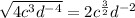
∴
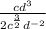
∵ In the same base with multiplication we add the power,
in same base with division we subtract the power
∴
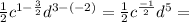
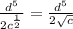 ⇒
⇒
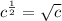
∴ The answer is (b) ⇒