Question

15 points!!!
kinda rusty with triangles. scratch that. really rusty.

​

Answer 1

Well to start off all sides are gonna be 20. To find area it’s lxw so 20•20=400

Dives 400 by 12 and you get 33.333333333 so you round that to the nearest whole foot and you get 33 feet

Answer 2

Consider the attached figure. The height CD cuts the triangle exactly in half. This means that

`\overline{AD}=\overline{BD}=(1)/(2)\overline{AB}=10`

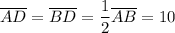
Moreover, since CD is the height of the triangle, we know that ACD is a right triangle. We know the hypothenuse AC to be 20 feet because it is a side of the triangle, and we just found out that AD is 10. We can use the pythagorean theorem to deduce

`\overline{CD}=\sqrt{\overline{AC}^2-\overline{AD}^2}=√(400-100)=√(300)`

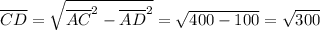
So, the area is

`A=(bh)/(2)=\frac{\overline{AB}\cdot\overline{CD}}{2} = (20\cdot√(300))/(2)=10√(300)\approx 173`