Hello!
The answer is:
b.
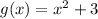
Why?
To find what's the equation of the red graph, first, we need to find a function that intercepts the y-axis at 3 and its vertex is located at (0,3)
We must remember that the constant value in a quadratic equation (c) will tell us where the function intercepts the y-axis, so, we are looking for an equation which has a constant value equal to 3, it discards the options a, c and d, so the correct option would be the option b.
Option b function:
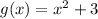
Where,

Let's check if the option b is the correct option:
First, let's find the axis intercepts:
Y-axis intercept

X-axis intercept
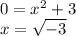
There is no x-axis intercepts since the square roots of negative numbers does not exists in the real numbers.
Finding the vertex coordinates:
The x coordinate of the vertex can be found using the following equation:
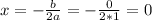
The x coordinate of the vertex is located at x=0, so to find the y-coordinate we must substitute the x value into the parabola equation, so

So, the y coordinate of the vertex is located at y=3
Therefore, the vertex of the function is (0,3)
Hence, the calculated values of the option b match with the given graph.
The correct option is: b.
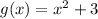
Have a nice day!