Answer:
Explanation:
Given: AD≅AO
To find: m∠OAD and m∠DBA.
Solution: It is given that AD≅AO, and also OA≅OD (Radius of circle), therefore ΔAOD is an equilateral triangle.
Hence, m∠OAD=m∠ODA=m∠AOD=60°.
Now, we know that the intercepted angle is half of the central angle, thus
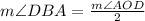
⇒
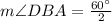
⇒
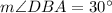
Hence, the measures of
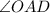 and
and
 are
are
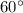 and
and
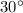 respectively.
respectively.