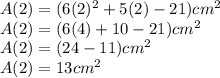Question

Write a polynomial expression, in simplified form, that represents the AREA of the blanket and use the expression to evaluate the AREA of the blanket if x = 2.

Answer 1

Polynomial expression that represents the area of blanket:

`A(x)=(6x^2+5x-21)cm^2`

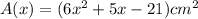
If
`x=2`:
`A(2)=13cm^2`

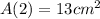
Explanation:

The area of the rectangle can be calculated with the formula:

`A=lw`

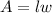
Being l the lenght of the rectangle and w the width of the rectangle.

In this case, the lenght and the width are represented with:

`l=(3x+7)cm`

`w=(2x-3)cm`

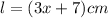
Substitute them into
`A=lw`:

`A(x)=(3x+7)(2x-3)`

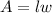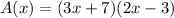
Then:

Use Distributive property (Remember the Product of powers property:
`b^a*b^c=b^((a+c))` ):

`A(x)=(3x+7)(2x-3)\\A(x)=6x^2-9x+14x-21`

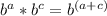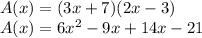
Add like terms:

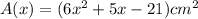`A(x)=(6x^2+5x-21)cm^2` (Simplied form)

Evaluate
`x=2`:

`A(2)=(6(2)^2+5(2)-21)cm^2\\A(2)=(6(4)+10-21)cm^2\\A(2)=(24-11)cm^2\\A(2)=13cm^2`