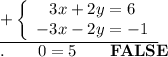Question

asked Jan 10, 2020 167k views

1 Answer

Mahmoud Fayez · Answer 1 · 2020-01-16T09:43:19+0000

Explanation:

We transform the system of equations to the form:

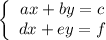
$\left\{\begin{array}{ccc}ax+by=c\\dx+ey=f\end{array}\right$

Where a & b and d & e are relatively prime number.

1.

If a ≠ d or b ≠ e then the system of equations has one solution.

Example:

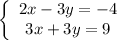
$\left\{\begin{array}{ccc}2x-3y=-4\\3x+3y=9\end{array}\right$

Add both sides of equations:

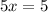5x=5 divide both sides by 5

x=1

Substitute it to the second equation:

3(1)+3y=9

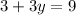3+3y=9 subtract 3 from both sides

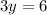3y=6 divide both sides by 3

y=2

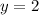
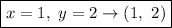
$\boxed{x=1,\ y=2\to(1,\ 2)}$

If a = d and b = e and c = f then the system of equations has infinitely many solutions.

Example:

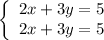
$\left\{\begin{array}{ccc}2x+3y=5\\2x+3y=5\end{array}\right$

Change the signs in the second equation. Next add both sides of equations:

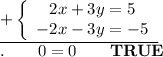
$\underline{+\left\{\begin{array}{ccc}2x+3y=5\\-2x-3y=-5\end{array}\right}\\.\qquad0=0\qquad\bold{TRUE}$

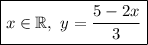
$\boxed{x\in\mathbb{R},\ y=(5-2x)/(3)}$

If a = d and b = e and c ≠ f then the system of equations has no solution.

Example:

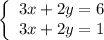
$\left\{\begin{array}{ccc}3x+2y=6\\3x+2y=1\end{array}\right$

Change the signs in the second equation. Next add both sides of equations:

$\underline{+\left\{\begin{array}{ccc}3x+2y=6\\-3x-2y=-1\end{array}\right}\\.\qquad0=5\qquad\bold{FALSE}$