Question

the sum of three numbers is 78. the third number is 3 times the first. the first number is 7 more than the second. what are the numbers?

Answer 1

17

Explanation:

x+3x+x-7=78

5x-7=78

5x=78+7

5x=85

x=85/5

x=17

Answer 2

The three numbers are 17, 10 and 51.

Explanation:

Let the first, second, and third numbers be
`x`,
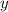`y`, and
`z` respectively.

• From the question, we know:

sum of the numbers is 78.

∴
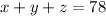`x + y + z = 78` ----------(1st equation)

Let's express both
`x` and
`z` in terms of
`\bf y` :

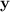• We know that:

the third number is 3 times the first.

∴
`z = 3x`

⇒
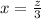`x = (z)/(3)` ----------(2nd equation)

• We also know that:

the first number is 7 more than the second.

∴
`\boxed{x = 7 + y}`

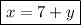
Substituting
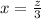`x = (z)/(3)` (from 2nd equation)

⇒
`(z)/(3) = 7 + y`

⇒
`\boxed{z = 21 + 3y}`

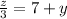
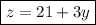
• We can now substitute
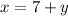`x = 7 + y` and
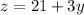`z = 21 + 3y` into the first equation:

`x + y + z = 78`

⇒
`(7 + y) + y + (21 + 3y) = 78`

⇒
`5y + 28 = 78`

⇒
`5y = 50`

⇒
`y = \bf 10`

∴
`x = 7 + 10\\`

⇒
`x = \bf 17`

`z = 21 + 3(10)`

⇒
`z = \bf 51`

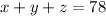
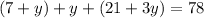
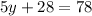
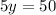
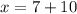
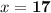
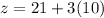
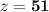
∴ The three numbers are 17, 10 and 51.