Question

The slope of the tangent to a curve at any point (x, y) on the curve is x divided by y. Find the equation of the curve if the point (2, −3) is on the curve. x2 + y2 = 13 x2 + y2 = 25 x2 − y2 = −5 x2 − y2 = 5

Answer 1

The correct option is D

Explanation:

Edge2020

Answer 2

`x^2-y^2=-5`

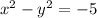
Explanation:

The problem tells us that the slope of the tangent to a curve at any point
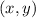`(x, y)` on the curve is x divided by y, that is:

`m=(x)/(y)`

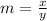
We also know that the point
`(2,-3)` is on the curve. By taking a look on the options this point lies on both equations, namely:

`x^2+y^2=13 \ because \ (2)^2+(-3)^2=13 \\ \\ x^2-y^2=-5 \ because \ (2)^2-(-3)^2=-5`

We know that the derivative is the slope of the tangent line to the graph of the function at a given point. So taking the derivative of both equations we have:

`(d)/(dx)(x^2+y^2)=(d)/(dx)(13) \\ \\ \therefore 2x+2y(dy)/(dx)=0 \\ \\ \therefore m=(dy)/(dx)=-(x)/(y)`

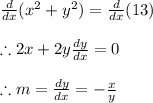
And:

`(d)/(dx)(x^2-y^2)=(d)/(dx)(-5) \\ \\ \therefore 2x-2y(dy)/(dx)=0 \\ \\ \therefore m=(dy)/(dx)=(x)/(y)`

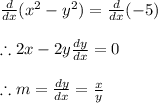
So
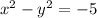`x^2-y^2=-5` also meets the requirement of the condition the slope of the tangent to a curve at any point (x, y) on the curve is x divided by y. Therefore this is the correct option.