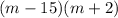Question

Which expression is equivalent to m^2-13m-30?

(m – 15) (m + 2)
(m – 10) (m – 3)
(m + 15) ( m – 2)
(m + 10) (m + 3)

Answer 1

`(m-15)(m+2)`

Explanation:

The given expression is

`m^2-13m-30`

Split the middle term

`m^2-15m+2m-30`

Factor

`m(m-15)+2(m-15)`

Factor further to obtain;

`(m-15)(m+2)`

The correct answer is A.

Answer 2

Answer: First option

Explanation:

You have the quadratic equation given in the problem:

`m^2-13m-30`

To find an equivalent expression you cacn factorize. Find two numbers whose sum is -13 and whose product is -30.

These numbers would be -15 and 2.

Therfore, you obtain the following equivalent expression:

`(m-15)(m+2)`

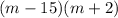
If you don't want to apply the method above, you can use the quadratic formula:

`x=(-b+/-√(b^2-4ac))/(2a)`

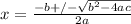
Where:

`a=1\\b=-13\\c=-30`

When you susbstitute values you obtain that:

`x=15\\x=-2`

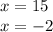
Then you can rewrite the equation as
`(m-15)(m+2)`