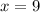Question

Determine all numbers at which the function is continuous.

Answer 1

B: continuous at every real number except x = 9

Step-by-step explanation: EDGE 2020

Answer 2

Explanation:

If the graph of any function is an unbroken curve, then the function is continuous. Let's study the function at the the point [/tex]x=5[/tex]:

At this point the function has the following value:

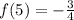`f(5)=-(3)/(4)`, so the function in fact exists here, but let's find the limit here using:

`f(x)=(x^2-7x+10)/(x^2-14x+45)`

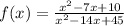
So:

`\underset{x\rightarrow5}{lim}(x^2-7x+10)/(x^2-14x+45)`

By factoring out this function we have:

`\underset{x\rightarrow5}{lim}((x-2)(x-5))/((x-5)(x-9)) \\ \\ \therefore \underset{x\rightarrow5}{lim}((x-2))/((x-9)) \\ \\ \therefore ((5-2))/((5-9))=-(3)/(4)`

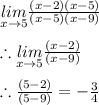
Since
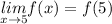`\underset{x\rightarrow5}{lim}f(x)=f(5)` then the function is continuous here.

Let's come back to our function:

`f(x)=(x^2-7x+10)/(x^2-14x+45)`

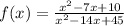
If we factor out this function we get:

`f(x)=((x-2))/((x-9))`

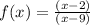
Notice that at x = 9 the denominator becomes 0 implying that at this x-value there is a vertical asymptote. The graph of this function is shown below and you can see that at x = 9 the function is not continous

Therefore, the answer is:

b. continous at every point exept
`x=9`