Question

What is the sum of the geometric series sigma 15,x=0, 2(1/3)x​

Answer 1

`\sum_(x=0)^(15)2((1)/(3))^x=3.0`

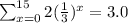
Explanation:

We want to evaluate:

`\sum_(x=0)^(15)2((1)/(3))^x`

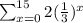
When x=0, we obtain the first term of the geometric series as

`a_0=2((1)/(3))^0`

The common ratio of this geometric series is
`r=(1)/(3)`

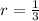
The sum of the first n-terms of a geometric series is

`S_n=(a(1-r^n))/(1-r)`

From x=0 to x=15, we have 16 terms.

The sum of the first 16 terms of the geometric series is

`S_(16)=(a(1-((1)/(3))^(16)))/(1-(1)/(3))=2.99999993031`

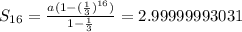
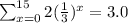`\sum_(x=0)^(15)2((1)/(3))^x=3.0` to the nearest tenth.