Question

Show me the graph of
10x + 7y < 49

Answer 1

Answer: The graph is attached.

Explanation:

1. Solve for y, as following:

`10x+7y<49\\7y<-10x+49\\y<-(10)/(7)x+(49)/(7)\\\\y<-(10)/(7)x+7`

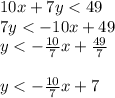
2. The equation of the line in slope intercept form is:

`y=mx+b`

Where m is the slope and b is the y-intercept.

3. In this case the equation of the line is:

`y=-(10)/(7)x+7`

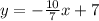
then:

`m=-(10)/(7)\\\\b=7`

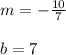
4. Find the x-intercept. Make y=0. Then:

`0=-(10)/(7)x+7\\(10)/(7)x=7\\x=4.9`

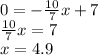
5. Then, plot the line that passes through the points (0,7) and (4.9, 0).

6. The symbol of the inequality is < therefore, the line must be dashed and indicates that the region under the line must be shaded.

Then you obtain the graph attached.