Answer:
The sum using summation notation is given by:
Summation of two times negative three to the power of n from n equals zero to infinity.
i.e. numerically it is given by:
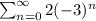
Explanation:
The alternating series is given by:
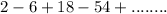
The series could also be written in the form:
