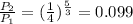Answer:
e) 0.099
Step-by-step explanation:
For an adiabatic transformation, we have:
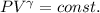
where
P is the gas pressure
V is the volume
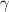 is the adiabatic index, which is
is the adiabatic index, which is
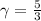 for an ideal monoatomic gas
for an ideal monoatomic gas
The previous law can also be rewritten as
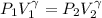
or
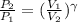
where we know that
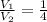
because the volume has increased by a factor 4.0. Substituting into the equation, we find by which factor the pressure has changed: