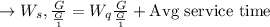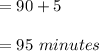Question

Pop-up Restaurant

A new pop-up restaurant serving high-end street tacos just opened and is expected to have high demand based on the chef's prior restaurant experience. The pop-up restaurant has only one window where customers order and receive their food. It takes an average of 5 minutes to serve a customer. There is no seating available so the customer exits the system after receiving their order. Due to the creative marketing strategy of "hiding" the restaurant location, only 10 customers arrive per hour. There is no specific pattern to the distribution of time between arrivals or service times, but from historical data from prior pop-ups, the coefficient of variation for time between arrivals is 2.58 and service time is 0.75. For new customers, how long do they have to wait in total before they leave with their food?
A. 40 minutes.B. 100 minutes.C. 0 minutes.D. 90 minutes.E. 10 minutes.F. 95 minutes.
G. 45 minutes.H. 20 minutes.I. 50 minutes.J. 15 minutes.

Answer 1

The answer is "Option F".

Step-by-step explanation:

The arrival rate
`(\lambda) = 10 \ / \ hour`

The service rate
`(\mu) = 1 \ in \ 5 \ minutes = 12\ /\ hour`

The time of waiting at queue

`(M)/((M)/(1)) \ queue, \ W_q, \\\\ (M)/((M)/(1)) = (\lambda)/( \mu * (\mu - \lambda))`

`= (10)/((12 * (12 - 10))) \\\\ = 0.4167 \ hours \\\\ = 25 \ minutes`

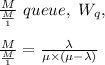
It was not a queue for
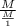`(M)/((M)/(1))`. This is a
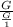`(G)/((G)/(1))` queue so because intercom or time intervals differ coefficient is given.

`\to c_a = 2.58\\\\\to c_e = 0.75`

`\to W_q , (G)/((G)/(1)) = ((c_(a)^2 + c_(e)^2))/(2) * W_q (M)/((M)/(1))`

`= ((2.58^2 + 0.75^2))/(2) * 25 \\\\ = ((6.6564 + 0.5625))/(2) * 25 \\\\ = 3.60945 * 25\\\\ = 90.23625\\\\ = 90 \ minutes`

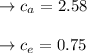
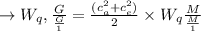
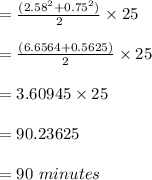
Therefore, the entire waiting time even before order is issued,

`\to W_s , (G)/((G)/(1)) = W_q (G)/((G)/(1)) + \text{Avg service time}`

`=90+5\\\\=95 \ minutes`