Question

50 POINTS! If the moon were twice as massive but twice as far from Earth, high tides on Earth would be – (think of it’s force)

a. higher
b. lower
c. no different

Answer 1

The answer would be C. If its twice as massive, AND twice as far, nothing would really change.

Answer 2

If the moon were twice as massive but twice as far from Earth, high tides on Earth would be lower.

Answer: Option B

Step-by-step explanation:

The occurrence of high tides on Earth is due to the gravitational force of moon acting on the sea water. So the gravitational force of moon during full moon day will be maximum as the distance between Earth and Moon will be minimum during this time and thus the moon’s gravity will be pulling the sea water towards itself leading to the formation of high tides.

As the high tides are formed due to the gravitational force acting between moon and Earth, the mathematical representation will be

`F=\frac{G M_{\text {moon }} M_{\text {Earth}}}{d^(2)}`

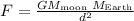
Let the F be the normal gravitational force acting between moon and Earth with
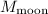`M_{\text {moon }}` and
`M_{\text {earth }}` as the mass of moon and Earth, respectively and d be the distance of separation of moon from Earth.

Now if we consider the special case given here where the mass of moon is doubled and also the distance of separation of moon from the earth is also doubled. So the new gravitational force with the parameters and comparing we get

`F^(\prime)=\frac{G M_{\text {moon }}^(\prime) M_{\text {earth }}}{d^(\prime 2)}`

`F^(\prime)=\frac{2 * G * M_{\text {moon}} * M_{\text {earth}}}{4 d^(2)}`

`F^(\prime)=(1)/(2) F`

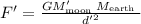
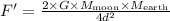
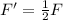
So as the gravitational force between Earth and moon will be reduced to half on doubling the distance of separation as well as mass of the moon, the occurrence of high tides will be lower with the given conditions.