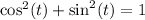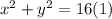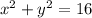Question

Eliminate the parameter.
x = 4 cos t, y = 4 sin

Answer 1

ANSWER


`{x}^(2) + {y}^(2) = 16`

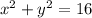
Step-by-step explanation

We want to eliminate the parameter from the equation:


`x = 4 \cos(t)...(1)`

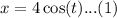
and


`y = 4 \sin(t)...(2)`

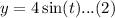
Square both sides of the first equation to get,


`{x}^(2) = (4 \cos(t) )^(2)`


`{x}^(2) = 16 \cos^(2) (t)...(3)`

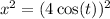
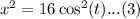
Squaring the second equation gives;


`{y}^(2) = {(4 \sin(t) )}^(2)`


`{y}^(2) = 16 \sin^(2) (t)...(4)`

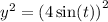
Add equation (3) and (4).

This implies that;


`{x}^(2) + {y}^(2) = 16 \cos^(2) (t) + 16 \sin^(2) (t)`

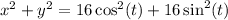
Factor the right hand side


`{x}^(2) + {y}^(2) = 16( \cos^(2) (t) + \sin^(2) (t))`

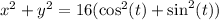
Recall that;


`\cos^(2) (t) + \sin^(2) (t) = 1`


`{x}^(2) + {y}^(2) = 16( 1)`


`{x}^(2) + {y}^(2) = 16`