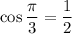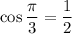
so you have
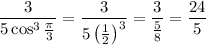
###
If you don't remember the value of
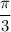 off the top of your head, it's possible to derive it with some identities and knowing that
off the top of your head, it's possible to derive it with some identities and knowing that
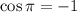 .
.
Consider the expression
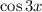 . With the angle sum identity, we have
. With the angle sum identity, we have
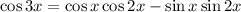
and the double angle identities give
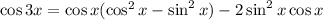
Write everything in terms of cosine:
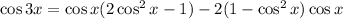
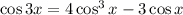
Now let
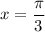 . Then
. Then
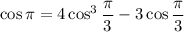
Let
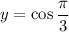 . Then
. Then
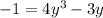
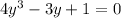
The rational root theorem suggests some possible roots are
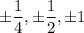
and checking all of these, we find that
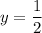 is among the solution set. In fact,
is among the solution set. In fact,
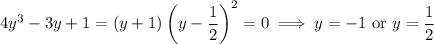
We have
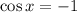 only for odd multiples of
only for odd multiples of
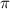 , so it follows that
, so it follows that