Question

What is the correct inverse function for f(x)=In(3x)

Answer 1

`{f}^( - 1) (x) = \frac{ {e}^(x) }{3}`

EXPLANATION

The given logarithmic function is

`f(x) = ln(3x)`

Let

`y = ln(3x)`

Interchange x and y.

`x = ln(3y)`

Solve for y.

`{e}^(x) = {e}^( ln(3y) )`

`{e}^(x) = 3y`

Divide both sides by 3.

`\frac{ {e}^(x) }{3} = y`

Therefore

`{f}^( - 1) (x) = \frac{ {e}^(x) }{3}`

Answer 2

`f^(-1)(x)=(e^x)/(3),\ x\in(-\infty,\infty),\ y>0`

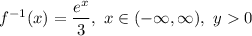
Explanation:

Consider the function
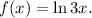`f(x)=\ln 3x.` the domain of this function is x>0 and the range of this function is all real numbers. The inverse function has the domain all real numbers and the range y>0.

If

`y=\ln 3x,`

then

`3x=e^y,\\ \\x=(e^(y))/(3).`

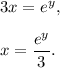
Change x into y and y into x:

`y=(e^x)/(3).`

Thus, the inverse function is

`f^(-1)(x)=(e^x)/(3).`