Question

The difference of two numbers is 20 and their product is 125, what is the answer?

Answer 1

Solution 1: The numbers are 25 and 5

Solution 2: The numbers are -5 and -25

Explanation:

We have 2 unknown numbers, then we can define them as:

x: Unknown number 1

y: Unknown number 2

The problem states that "the difference of two numbers is 20". We can translate this to x - y = 20

We also know that "their product is 125". We can translate this to x . y = 125

Putting both equations together, we get the following system of equations

`\left \{ {{x - y = 20} \atop {x y=125}} \right.`

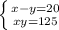
Now, to solve this system of equations we can use the Substitution Method.

We can solve 1st equation for x, by adding y to both sides

x - y + y = 20 + y

x = 20 + y

We can substitute x by 20 + y on the 2nd equation

(20 + y) . y = 125

Applying distributive property on the left side

20y + y² = 125

Substracting 125 to both sides and rearranging the terms, we get

20y + y² - 125 = 125 -125

y² + 20y - 125 = 0

We can apply the quadratic equation attached to solve this (with a = 1, b = 20, c = -125).

( -20 ± √(20² - 4 . 1 . -125) ) / ( 2. 1 ) =

( -20 ± √(400 + 500) ) / ( 2) =

( -20 ± √900 ) / ( 2) =

( -20 ± 30 ) / ( 2) =

We get 2 results:

• y1 = (-20 + 30) / 2 = 5
• y2 = (-20 - 30) / 2 = -25

For each of these values of y, we can find the corresponding value of x:

• x1 = 20 + y1 = 20 + 5 = 25
• x2 = 20 + y2 = 20 + (-25) = -5

Answer 2

find prime factors to get the inbetween numbers for product, and choose the one that has a difference of 20, and it should be 5 and 25, both requirements are met.