Answer:
$70,300
Explanation:
The amount Kaydence saved is the value of an arithmetic series with first term 100 and common difference 100. The number of terms in the sum is 37. The formula for the sum can be used.
Sum of an arithmetic series
The formula for the sum of n terms of an arithmetic series is ...
Sn = (2a1 +d(n -1))(n/2) . . . . . . first term a1, common difference d
Application
The number of terms being added is ...
2050 -2014 +1 = 37 . . . . . . years Kaydence made deposits
The formula with a1=100, d=100, and n=37 is ...
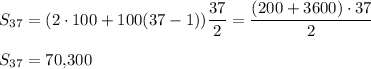
Kaydence would have saved $70,300 by the end of Jan 1, 2050.