Question

What is the end behavior of the function f(x) = 2x^4 + 6x^8 - 9x^9 - 5x?

Answer 1

`\lim_(x \to \infty) f(x)` = -∞

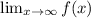[/tex]\lim_{x \to \ -infinity} f(x)[/tex] = +∞

Explanation:

First it will be helpful to rearrange the term by power of x like so :

f(x) = - 9x^9 + 6x^8 + 2x^4 - 5x

By "end behavior" we mean what happens when x goes to +∞/-∞.

So we need to calculate
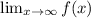`\lim_(x \to \infty) f(x)` and [/tex]\lim_{x \to \ -infinity} f(x)[/tex].

It is easy to think as just replacing x with a very big number.(lets say 10000)

And you will see that when x goes to -∞ you will get some very big positive number and when when x goes to +∞ you will get a very big negative number.