Question

Two wires are stretched between two fixed supports and have the same length. One wire A there is a second-harmonic standing wave whose frequency is 660 Hz. However, the same frequency of 660 Hz is the third harmonic on wire B. (a) Is the fundamental frequency of wire A greater than, less than, or equal to the fundamental frequency of wire B? Explain. (b) How is the fundamental frequency related to the length L of the wire and the speed v at which individual waves travel back and forth on the wire? (c) Do the individual waves travel on wire A with a greater, smaller, or the same speed as on wire B? Give your reasoning.

Answer 1

(a) Greater

The frequency of the nth-harmonic on a string is an integer multiple of the fundamental frequency,
`f_1`:

`f_n = n f_1`

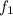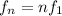
So we have:

- On wire A, the second-harmonic has frequency of
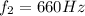`f_2 = 660 Hz`, so the fundamental frequency is:

`f_1 = (f_2)/(2)=(660 Hz)/(2)=330 Hz`

- On wire B, the third-harmonic has frequency of
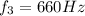`f_3 = 660 Hz`, so the fundamental frequency is

`f_1 = (f_3)/(3)=(660 Hz)/(3)=220 Hz`

So, the fundamental frequency of wire A is greater than the fundamental frequency of wire B.

(b)
`f_1 = (v)/(2L)`

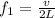
For standing waves on a string, the fundamental frequency is given by the formula:

`f_1 = (v)/(2L)`

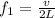
where

v is the speed at which the waves travel back and forth on the wire

L is the length of the string

(c) Greater speed on wire A

We can solve the formula of the fundamental frequency for v, the speed of the wave:

`v=2Lf_1`

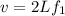
We know that the two wires have same length L. For wire A,
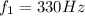`f_1 = 330 Hz`, while for wave B,
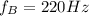`f_B = 220 Hz`, so we can write the ratio between the speeds of the waves in the two wires:

`(v_A)/(v_B)=(2L(330 Hz))/(2L(220 Hz))=(3)/(2)`

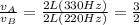
So, the waves travel faster on wire A.