Question

Estimate the limit

A
B
C
D

Answer 1

C.
`\lim_{x\rightarrow f(x)=2`

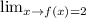
Explanation:

Given problem is
`\lim_{x\rightarrow (\pi)/(4)}(tan(x)-1)/(x-(\pi)/(4))`.

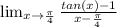Now we need to evaluate the given limit.

If we plug
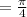`\x=(\pi)/(4)`, into given problem then we will get 0/0 form which is an indeterminate form so we can apply L Hospitals rule

take derivative of numerator and denominator

`\lim_{x\rightarrow (\pi)/(4)}(tan(x)-1)/(x-(\pi)/(4))`

`=\lim_{x\rightarrow (\pi)/(4)}(sec^2(x)-0)/(1-0)`

`=(sec^2((\pi)/(4))-0)/(1-0)`

`=((√(2))^2)/(1)`

`=(2)/(1)`

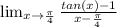
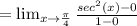
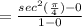
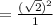
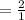
=2

Hence choice C is correct.