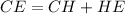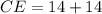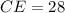Question

If J is the centroid of cde, de=52, fc=15, he=14, find each missing measure

Answer 1

`DG = 26`

`GE = 26`

`DF = 15`

`CH = 14`

`CE = 28`

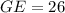
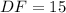
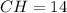
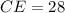
Explanation:

The figure has been attached, to complement the question.

`DE = 52`

`FC = 15`

`HE = 14`

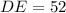
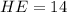
Given that J is the centroid, it means that J divides sides CD, DE and CE into two equal parts respectively and as such the following relationship exist:

`DF = FC`

`CH = HE`

`DG = GE`

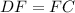
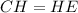
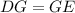
Solving (a): DG

If
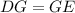`DG = GE`, then

`DE = DG + GE`

`DE = DG + DG`

`DE = 2DG`

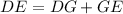
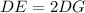
Make DG the subject

`DG = (1)/(2)DE`

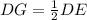
Substitute 52 for DE

`DG = (1)/(2) * 52`

`DG = 26`

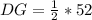
Solving (b): GE

If
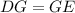`DG = GE`, then

`GE = DG`

`GE = 26`

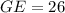
Solving (c): DF

`DF = FC`

So:

`DF = 15`

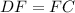
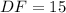
Solving (d): CH

`CH = HE`

`CH = 14`

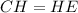
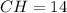
Solving (e): CE

If
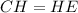`CH = HE`, then

`CE = CH + HE`

`CE = 14 + 14`

`CE = 28`