(a) 11.1 m/s
The acceleration of the skier is given by:
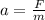
where F = 92 N is the net force and m = 68 kg. Substituting,
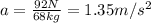
After 8.2 s, the speed of the skier is
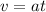
where
a = 1.35 m/s^2 is the acceleration
t = 8.2 s is the time
Substituting,
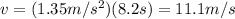
(b) 10.0 m/s
In this section of the hill, the net force is F = -22 N backwards. So, the acceleration of the skier is
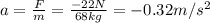
When starting this section, the skier is moving at u = 11.1 m/s. So, the final speed will be:

And substituting t=3.5 s, we find

(c) 237.9 m
The distance travelled by the skier in the downhill section is
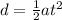
where a = 1.35 m/s^2 and t = 8.2 s. Substituting,
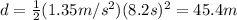
The distance travelled by the skier in the levelled out section is given by

where
v = 0 is the final speed
u = 11.1 m/s is the initial speed
a = -0.32 m/s^2 is the acceleration
d is the distance
Solving for d,
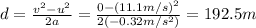
So, the total distance is
d = 45.4 m + 192.5 m = 237.9 m