Question

What is the solution set?

Answer 1

❣ [̲̅R̲̅][̲̅e̲̅][̲̅f̲̅][̲̅e̲̅][̲̅r̲̅]

[̲̅T̲̅][̲̅h̲̅][̲̅e̲̅]

[̲̅A̲̅][̲̅t̲̅][̲̅t̲̅][̲̅a̲̅][̲̅c̲̅][̲̅h̲̅][̲̅m̲̅][̲̅e̲̅][̲̅n̲̅][̲̅t̲̅] ❣

❣❣... ℏ✺℘ḙ !т ℏḙℓ℘ṧ ʏ✺ṳ...❣❣

Answer 2

The possible solution that is obtained from the system of equation are:

(1,3) and (6,13)

Explanation:

We are asked to find the solution set of the given system of equation as:

`y=x^2-5x+7-----------(1)`

and
`y=2x+1--------(2)`

We know that the solution of the system of equations is the possible set of x and y-values that satisfy both the equations.

Or we may say the point of intersection of the graph that is obtained from both the equations.

We solve the system by substitution method as:

We put the value of y from equation (1) in equation (2) to obtain:

`x^2-5x+7=2x+1`

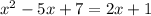
which is further written by combining the like terms as:

`x^2-5x-2x+7-1=0\\\\x^2-7x+6=0\\\\x^2-6x-x+6=0\\\\x(x-6)-1(x-6)\\\\(x-1)(x-6)=0`

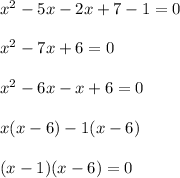
Hence, we get the possible values of x as:

x=1 and x=6

• Also the value of y when x=1 is:

y=2×1+1=2+1 ( Putting the value of x in equation (2))

y=3

• when x=6 we have the value of y as:

y=2×6+1

y=13

Hence, the possible solutions are:

(1,3) and (6,13)