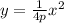Question

The equation for a parabola with directrix y = –p and focus (0, p) is:

Answer 1

`y=(1)/(4p)x^(2)`

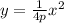
Explanation:

∵ The directrix is y = -p

∵ The focus is (0 , p)

∵ (x , y) is a general point on the parabola

∵ The distance between (x , y) and the directrix = the distance

between (x , y) and the focus

By using the rule of distance:

∵ (y - -p)² = (x - 0)² + (y - p)²

∴ (y + p)² = x² + (y - p)²

∴ y² + 2py + p² = x² + y² - 2py + p²

∴ 2py + 2py = x²

∴ 4py = x² ⇒ ÷ 4p in both sides

∴
`y=(1)/(4p)x^(2)`