Question

Point A (-7,-2) is rotated 270 counterclockwise and then shifted down 3 units. What are to coordinates of K’

Answer 1

-2,4

Explanation:

i did it

Answer 2

K'= (-2, 4)

Explanation:

First we are going to rotate our point 270° counterclockwise.

The rule for a 270° counterclockwise rotation is
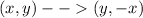`(x,y)-->(y,-x)`, which means that we just need to interchange the coordinates of the point and change the sign of the x-coordinate:

`(x,y)-->(y,-x)`

`(-7,-2)-->(-2,-7)`

`(-7,-2)-->(-2,-(-7))`

`(-7,-2)-->(-2,7)`

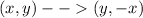
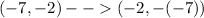
Now, to shift the point 3 units down, we just need to subtract 3 units from the new y-coordinate of our resulting point form the previous procedure:

`(x,y)-->(x,y-3)`

`(-2,7)-->(-2,7-3)`

`(-2,7)-->(-2,4)`

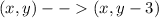
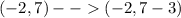
We can conclude that the coordinates of K' are (-2, 4)