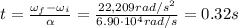Answer:
0.32 s
Step-by-step explanation:
Initial angular speed:
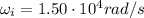
Final angular speed:
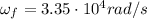
Angular rotation:
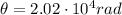
The angular acceleration of the drill can be found by using the equation:
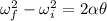
Re-arranging it, we find
 , the angular acceleration:
, the angular acceleration:
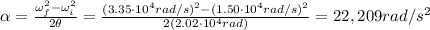
Now we want to know the time t the drill takes to accelerate from
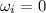
to
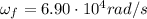
This can be found by using the equation
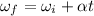
where
 is the angular acceleration we found previously. Solving for t,
is the angular acceleration we found previously. Solving for t,