Question

Type the correct answer in each box.Use numerals instead of words. If necessary, use / for the fraction bar.

Line AB and Line BC form a right angle at their point of intersection, B.

If the coordinates of A and B are (14, -1) and (2, 1), respectively, the y-intercept of Line AB is _____ and the equation of is y = ___x+___.

If the y-coordinate of point C is 13, its x-coordinate is ___.

Answer 1

y intercept is 1 1/3

equation is y = -1/6x + 4/3

x coordinate is -70 (-70,13)

Explanation:

find M

m = 1 - (-1)/ 2 -1 4

m = -2/12 = -1/6

Find y intercept--Plug m and one point from above into y = mx + b

1 = - 1/6 (2) + b

1 = -2/6 + b

1 2/6 = b

1 1/3 = b

4/3 = b

To find the x coordinate if y is 13

13 = -1/6 x + 4/3

11 2/3 = -1/6 x

-70 = x

Answer 2

The y intercept of line AB =
`(0,(4)/(3))`

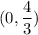
The equation of line AB will be

`y=(-1)/(6)x+(4)/(3)`

The x-coordinate of C = 4

Explanation:

The slope of line AB with coordinates of A and B are (14, -1) and (2, 1)

`m_1=(1-(-1))/(2-14)=(2)/(-12)=(1)/(-6)`

The equation of line AB will be

`(y-1)=(1)/(-6)(x-2)\\\\\Rightarrow y=(1)/(-6)(x-2)+1\\\\\Rightarrow\ y=(-1)/(6)x+(1)/(3)+1\\\\\Rightarrow y=(-1)/(6)x+(4)/(3)`

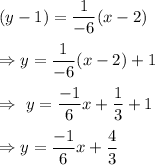
Put x=0, we get the
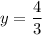`y=(4)/(3)` i.e.
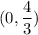`(0,(4)/(3))` is the y intercept of line AB.

Since, Line AB and Line BC form a right angle at their point of intersection, B. The the product of their slope must be -1.

Therefore, the slope of BC =
`m_2=(-1)/(m_1)=6`

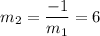
Let x coordinate of C be a,then the coordinates of C = (a,13)

Now, slope of BC with points B(2,1) and C(a,13) will be

`(13-1)/(a-2)=6\\\\\Rightarrow\ a-2=(12)/(6)\\\\\Rightarrow\ a-1=2\\\\\Rightarrow\ a=4`

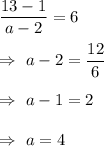
Hence, the x-coordinate of C = 4