Answer:
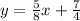
Explanation:
We are to write the slope intercept form of the equation which passes through the point (2, 3) and is parallel to the line
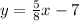 .
.
We know that the standard (slope-intercept) form of an equation of a line is given by:
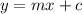
where
 is the slope and
is the slope and
 is the y-intercept.
is the y-intercept.
Since we are to find the equation of the line parallel to the given equation so its slope will be same as of
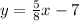 .
.
Finding the y-intercept:
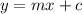
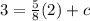
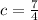
Therefore, the equation will be
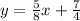 .
.