Answer:
44. 7 yr
Explanation:
The compound interest equation is
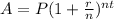
You don't give the frequency of compounding, so I will assume that it is once per year.
Data:
P = $40
r = 0.5 % = 0.005
n =1
Calculations:
(a) Calculate A
A = P + I = 40 + 10 = $50
(b) Calculate t
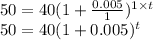
Divide each side by 40
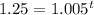
Take the logarithm of each side
log1.25 = tlog1.005
0.09691 = 0.002 166t
Divide each side by 0.002 166
t = 44.7 yr
The value of the stock will be $50 in 44.7 yr.