Question

(Please show steps)
Graph the logarithmic function y=log(x-2)

Answer 1

So the answer is (3, 0) on a graph.

Explanation:

What I use is a graphing calculator. It helps tremendously. It is called desmos.com. Hope this helps.

Answer 2

The given function is

`y=log(x-2)`

To graph any function, we just have to five arbitrary values to x-variable, and see the y-values that gives to formed coordinate pairs to graph them then.

In this case, the table that shows these values is gonna be

X Y

2.5 -0.3

3 0

3.5 0.2

4 0.3

4.5 0.4

Notice that we started from
`x=2.5`. The reason is beacuse the given logarithmic function is not defined for values equal or lower than 2, when taht happens, the function becoms undetermined. This means the domain of the given function has to be restricted to
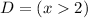`D= (x>2)`, otherwise the function won't be defined.

Next, we evalute the function for each case.

`x=2.5`

`y=log(x-2)=log(2.5-2)=log(0.5) \approx -0.3`

`x=3\\y=log(x-2)=log(3-2)=log(1)=0`

`x=3.5\\y=log(x-2)=log(3.5-2)=log(1.5) \approx 0.2`

`x=4\\y=log(x-2)=log(4-2)=log(2) \approx 0.3`

`x=4.5\\y=log(x-2)=log(4.5-2)=log(2.5) \approx 0.4`

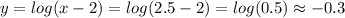
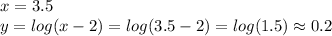
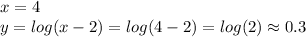
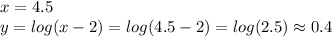
When you have the table completed, you proceed to graph each coordinate.

In this case, the graph of the logarithmic function would be as the image attached. That's all the process to graph the function.

(In the graph, you can observe how fast the function drops when is near to x=2, that's the undetermination behaviour we talk about lines above).