Answer:
1. B (obtuse)
2. Obtuse
3. 20.92
Explanation:
1.
We need to use the converse of the pythagorean theorem to solve this problem. Given that c is the longest side of a triangle, and a and b are the other two sides. The triangle is right triangle if

The triangle is acute triangle if
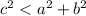
The triangle is obtuse triangle if
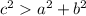
the longest side of this triangle is 47, so we check:
 , and
, and
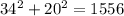
Hence, c^2 is GREATER than a^2 + b^2, so the triangle is obtuse.
2. Using the points we showed above, we can again summarize:
- If
 -- Right Triangle
-- Right Triangle - if
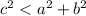 -- Acute Triangle
-- Acute Triangle - if
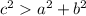 -- Obtuse Triangle
-- Obtuse Triangle
This triangle's c (longest side) is 5. Let's check:
5^2 = 25, and
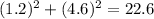
Hence, c^2 is GREATER than a^2 +b^2, so the triangle is obtuse.
3.
The side opposite of the 90 degree angle is the "hypotenuse", that is x. The side opposite the 35 degree angle is "opposite" side.
The trigonometric ratio that related "opposite" side to "hypotenuse" side is SINE. So we can write:
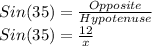
Now, cross multiplying and solving:
