Answer:
The function that has an inverse function is:
D.

Explanation:
We know that " A inverse of a function f(x) exist if it is both 1-1 and onto "
A)
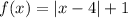
We know that the modulus function is not 1-1.
Since, there are two different 'x' such that the function have the same value.
Take x=1
and take x= 7
In both the cases we have: f(x)=4
Hence, the function does not has a inverse.
B)
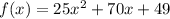
We know that a polynomial with even degree is not 1-1.
As it is symmetric about a line x=a
Hence, option: B is incorrect.
C)
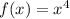
Again it is a polynomial of even degree.
Hence, it does not has a inverse.
D)

As the function is both 1-1 and onto.
Hence, the function has a inverse and the inverse function is calculated as:
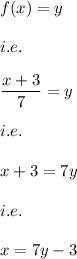
Hence, the inverse function is:
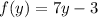
The answer is:
Option: D