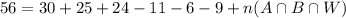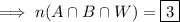Question

1. In a class of 60 students, a survey was conducted, 30 students had applied for Addis Ababa University, 25 students applied for Bahir Dar University and 24 students applied for Wachemo University. 11 students applied for both Addis Ababa and Bahir Dar Universities, 6 applied for both Addis Ababa and Wachemo Universities, 9 applied for both Wachemo and Bahir Dar Universities while 4 applied neither of the aforementioned universities. Find 1) number of student that applaid for all the university​

Answer 1

Let A, B, and W denote the sets of students apply to Addis Ababa Uni (A), Bahir Dar Uni (B), or Wachemo Uni (W). Let U denote the universal set of all students in the class.

We're given the cardinalities of several sets:

• total number of students:
`n(U) = 60`

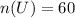
• A applicants:
`n(A) = 30`

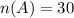
• B applicants:
`n(B) = 25`

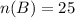
• W applicants:
`n(W) = 24`

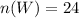
• A and B applicants:
`n(A\cap B) = 11`

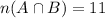
• A and W applicants:
`n(A \cap W) = 6`

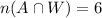
• B and W applicants:
`n(B\cap W) = 9`

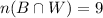
• non-applicants:
`n(U \setminus (A\cup B\cup W)) = 4`

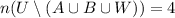
The last cardinality tells us
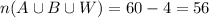`n(A\cup B\cup W) = 60-4 = 56` students applied anywhere at all.

We want to find
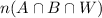`n(A\cap B\cap W)`, the number of students that applied to each of the three universities.

By the inclusion/exclusion principle,

`n(A\cup B\cup W) = n(A) + n(B) + n(W) \\\\~~~~~~~~~~~~~~~~~~~~~~~~ - n(A\cap B) - n(A\cap W) - n(B\cap W)\\ \\~~~~~~~~~~~~~~~~~~~~~~~~ + n(A\cap B\cap W)`

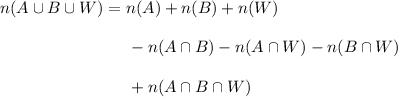
That is, we count up all the students in the sets A, B, and W, then subtract the number of students in each pairwise intersection to not double-count, then add back the number of students in the intersection of all three sets since it was removed in the previous step.

Now solve.

`56 = 30 + 25 + 24 - 11 - 6 - 9 + n(A\cap B\cap W)`

`\implies n(A\cap B\cap W) = \boxed{3}`