Question

This system has one solution.

y=8x−14,
y=x^2+4x−10
What is the y-coordinate of the solution? Enter your answer in the box.

Answer 1

y=2

Explanation:

Given that the system has one solution.

y=8x−14,

`y=x^2+4x−10`

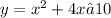
Now we need to find about what is the y-coordinate of the solution.

To find that plug value of y from first equation into 2nd equation

`8x−14=x^2+4x−10`

`0=x^2+4x−10-8x+14`

`0=x^2-4x+4`

`0=x^2-2x-2x+4`

`0=(x-2)(x-2)`

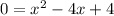
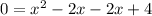
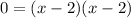
=> x-2=0 or x=2

Now plug x=2 into first equation

y=8x-14

y=8(2)-14

y=16-14

y=2

Hence final answer is y=2

Answer 2

Answer: It is 2.

Explanation:

Make both equation equal to each other and solve for x, as following:

- Add like terms.

- Factor the equation.

`8x-14=x^(2)+4x-10\\x^(2)+4x-10-8x+14=0\\x^2-4x+4=0\\(x-2)(x-2)=0\\(x-2)^2=0\\x=2`

Substitute the value of x obtained into any of the original equations to obtain the y-coordinate.

Then, this is:

`y=8(2)-14\\y=16-14\\y=2`