a. Let
 be a random variable representing the weight of a ball bearing selected at random. We're told that
be a random variable representing the weight of a ball bearing selected at random. We're told that
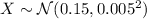 , so
, so
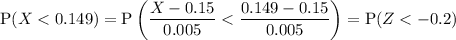
where
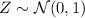 . This probability is approximately
. This probability is approximately
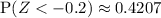
b. Let
 be a random variable representing the weight of the
be a random variable representing the weight of the
 -th ball that is selected, and let
-th ball that is selected, and let
 be the mean of these 4 weights,
be the mean of these 4 weights,
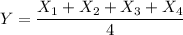
The sum of normally distributed random variables is a random variable that also follows a normal distribution,

so that
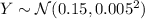
Then
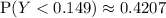
c. Same as (b).