Question

Which of the following are attributes of the function f(x)= |4(x-8)|-1 ?

Answer 1

Option 1 and 2.

Explanation:

Given : Function
`f(x)= |4(x-8)|-1`

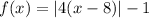
To find : Which of the following are attributes of the function?

Solution :

We find the domain, range , x-intercept and symmetry of the given function to match from given attributes.

Function
`f(x)= |4(x-8)|-1`

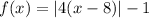
1) Domain is defined as the set of values in which function is defined.

Since, The given function for value x is under the absolute function so it is defined for all real numbers.

i.e.
`D=[(-\infty,\infty), x|x\in \mathbb R]`

2) The range is defined as the set of values that correspond with the domain.

i.e.
`R=[(-1,\infty), y|y\geq -1]`

3) x - intercept is defined as the value of x when y=0.

So,
`|4(x-8)|-1=0`

`|4(x-8)|=1`

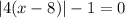
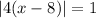
The values of x are
`((33)/(4),0), ((31)/(4),0)`

So, x-intercept exist.

4) Symmetry about x-axis

We show it by graphically as the vertex of equation is (8,0)

And if we construct a line x=8 the graph divides into two equal parts which means it is symmetrical at x=8.

Refer the attached figure below.

Therefore, From the following options, Option 1 and 2 are correct.