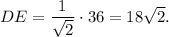Question

The length of triangle base is 36. The line which is parallel to the base divides the triangle into two equal area parts. Find a length of the segment between triangle legs.

Answer 1

`18√(2)`

Explanation:

Consider triangle ABC with the base AC=36. Let the line DE be parallel to the line AC. If DE||AC, then triangles ABC and DBE are similar. If k is the scale factor of these triangles, then

`(DE)/(AC)=(BG)/(BF)=k.`

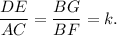
Thus,

`DE=k\cdot AC=36k,\\ \\BG=k\cdot BF.`

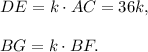
The area of the triangle ABC is

`A_(ABC)=(1)/(2)AC\cdot BF=(1)/(2)\cdot 36\cdot BF=18BF.`

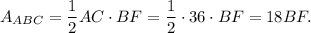
The area of the triangle DBE is

`A_(DBE)=(1)/(2)DE\cdot BG=(1)/(2)\cdot 36k\cdot kBF=18k^2BF.`

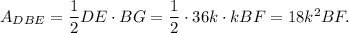
Since line DE divides triangle ABC in two equal area parts, we have that

`A_(DBE)=(1)/(2)A_(ABC),\\ \\18k^2BF=(1)/(2)\cdot 18BF,\\ \\k^2=(1)/(2),\\ \\k=(1)/(√(2))`

and

`DE=(1)/(√(2))\cdot 36=18√(2).`