Answer:
Choice C
eccentricity = 5/6
conic section; ellipse
directrix; x = -11/5
Explanation:
The first step is to write the polar equation in standard form by dividing both the numerator and denominator by 6;
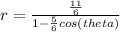
The eccentricity of the conic section is the coefficient of cos theta, thus;
e = 5/6
Since e lies between 0 and 1, the conic section is an ellipse.
To determine the equation of the directrix, we use the equation;
e*d = 11/6
5/6 *d = 11/6
d = 11/5
Since the conic section opens towards the right, the equation of the directrix becomes;
x = -11/5