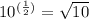Answer:
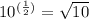
Explanation:
By definition you have that you can write:
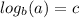
as following:
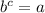
Therefore, keeping the information above on mind, you can write the following equivalent exponential equation for the exppresion given in the problem (
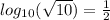 ):
):
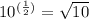
Thenrefore, the answer is: