2 Answers

Lehermj · Answer 1 · 2020-07-02T02:56:53+0000

Answer:

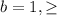
$b=1, \geq$

Explanation:

we know that

The absolute value function has two solutions

Observing the graph

the solutions are

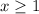$x\geq 1$ and
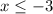
$x\leq -3$

First solution (case positive)

assume the symbol of the first solution and then compare the results

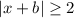
$\left|x+b\right|\ge2$

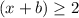
$(x+b)\ge2$

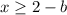
$x\ge2-b$

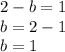
$2-b=1\\b=2-1\\ b=1$

Second solution (case negative)

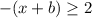
$-(x+b)\ge2$

Multiply by -1 both sides

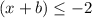
$(x+b)\leq-2$

substitute the value of b and compare the results

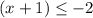
$(x+1)\leq-2$

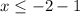
$x\leq-2-1$

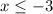$x\leq-3$ -------> is correct

Please log in or register to add a comment.