Question

Which statement describes the relationship, if any, that exists between triangle KLM and triangle NPQ?

1.) They are similar because their corresponding angles are congruent and their corresponding side lengths are in the ratio (3/2) from KLM to NPQ

2.) They are similar because their corresponding angles are congruent and their corresponding side lengths are in the ratio (2/1) from KLM to NPQ

3.) They are not similar because their corresponding angles are not congruent

4.) Thry are not similar because their corresponding side lengths are not proportional

Answer 1

i think it is 2

Explanation:

hope this helps i just finnished with this unit so my mind is still fresh

Answer 2

(B)

Explanation:

It is given that KLM and NPQ are the two triangles in which ∠L=∠P, ∠K=∠N and ∠M=∠Q. Also, KL=16, LM=22, KM=12, NP=8, PQ=11 and NQ=6.

Now, From ΔKLM and ΔNPQ, applying the basic proportionality theorem, we have

`(LK)/(NP)=(LM)/(PQ)=(KM)/(NQ)`

`(16)/(8)=(22)/(11)=(12)/(6)=(2)/(1)`

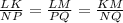
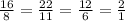
which holds, and thus the two triangles are similar as their corresponding sides are in the ratio 2:1 from KLM to NPQ.

Also, it is given that ∠L=∠P, ∠K=∠N and ∠M=∠Q that is the corresponding angles are congruent.

therefore, the two triangles similar because their corresponding angles are congruent and their corresponding side lengths are in the ratio 2:1 from KLM to NPQ.

Hence, option B is correct.